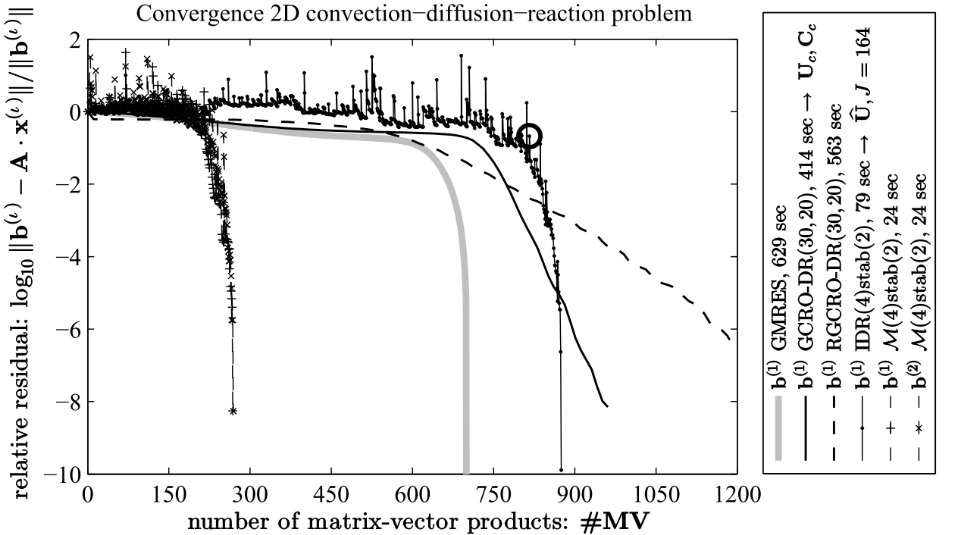
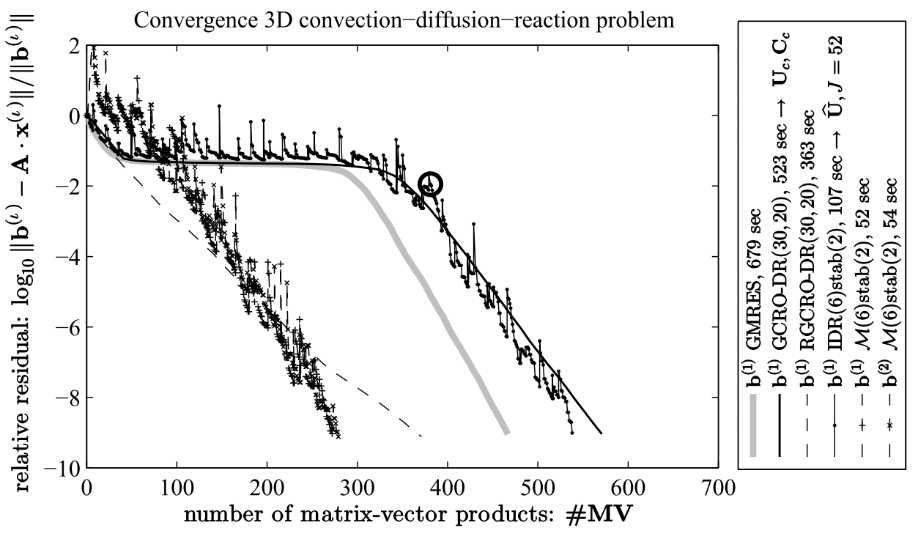
GMstab
GMstab is a robust implementation of IDR(s)stab(L) and M(s)stab(L). The method is based on an interior restarted GMRES method of length L*(s+1). The value for L is chosen adaptively between 1 and 2. Flying restart and convergence maintenance techniques are utilized in order to yield a maximum of robustness and superlinear convergence improvements. Please download, share and discuss.
Description of the method

IDR(s)stab(L) is a parametric short recurrence Krylov subspace method and the generalization of the most commonly used Krylov subspace methods for non-hermitian linear systems such as:
IDR methods use invariant-like subspaces S \subset C^N. The spaces satisfy A * (S \cap P^\perp) \subset S, where A is a system matrix and P is a small random subspace of C^N. From these spaces GMstab can be derived along the following lines:
  1. Building an oblique projector from A*S into S, one can build a GMRES method that operates in S.
  2. The Arnoldi decomposition from the interior GMRES method can be utilized to obtain orthogonal bases for the oblique projections of a successive Sonneveld space of S.
  3. Repeting the first two steps yields an iterative method.
Further developments in GMstab are that it automatically applies flying restarts (to achieve smaller true residual tolerances) and utilizes different convergence maintenance strategies by using adaptive values for L, modified minimum-residual polynomials in the stabilization step, and different implementations of the iterative loop for L=1 in order to avoid decoupling of the auxiliary vectors (i.e. keeping ||V-A*U|| small).

GMstab is presented in my Master's Thesis. Unfortunately, I cannot publish my thesis yet because the minimum processing time is not over.

You can find a Matlab implementation of GMstab under the following link: GMstab.m

Use the method as follows to solve two systems A*x1=b1, A*x2=b2.
[x1,hU] = IDRstabg3(A,b1,0*b1,1,1,1e-12,1000,10,1e-3);     % uses IDR(10)stab(L)
[x2] = IDRstabg3(A,b2,0*b2,1,1,1e-12,1000,10,hU);     % uses M(10)stab(L)

Solver programs used in my master thesis can be accessed under the following link: Solvers.zip
Some test cases refer to problem data that is available on the Matrix Market and the University of Florida Sparse Matrix Collection.

Below are some examples for superlinearity and termination behaviour of GMstab with and without M-space recycling for systems from discretized convetion-dominated PDEs. The figures are taken from Martin Neuenhofen, "Mstab: Stabilized Induced Dimension reduction for Krylov subspace recycling" .

Finite termination example.
Fig 1: Example that shows finite termination.

Example for superlinearity.
Fig 2: Example that shows superlinear convergence.



Contact via e-mail: MartinNeuenhofen@googlemail.com