Simple Finite Element Code

A simple code to assemble stiffness matrices for given 2D and 3D tetrahedral triangulations.
Finite element methods are often the method of choice when numerically solving (systems of) partial differential equations. Compared to finite differences, finite elements are suitable for more general problems (weak solutions) and they can be applied more flexible on complicated integration domains. However, in contrast to finite difference methods, finite element methods are more complicated to implement.

With SimpleFEM I try to provide a comprehensible code, consisting of less then 1000 lines, to assemble stiffness matrices and right-hand sides for various kinds of line-, surface- and volume-integrals for polynomial shape- and test-functions of first and second degree in two and three spatial dimensions. The emphasize lies on understandability, simplicity and modifiability.

To generate meshes for these assembles the distmeshnd routines of Persson and Strang are used, cf. [Per-Olof Persson and Gilbert Strang, A Simple Mesh Generator in MATLAB, SIAM Review Vol. 46 (2) 2004]. The code is distributed under GPL license and without any warranty to be anything more than a couple of characters.

The code is accessible under the following link: Simple_FEM.zip

Currently, I develop an adaptive multi-level triangulation in combination with shape-functions of arbitrary adaptive degree under the working title HiraFEM. The following images show examplary solutions in two and three spatial dimensions computed with SimpleFEM and HiraFEM.
Exemplary solution of a Poisson problem on a coarse and a fine grid.
Figure 1: Examplary solution of a Poisson problem on a pizza-shaped domain.
The solution exists only in a weak sense due to a singularity of the gradient in the concave edge.
---


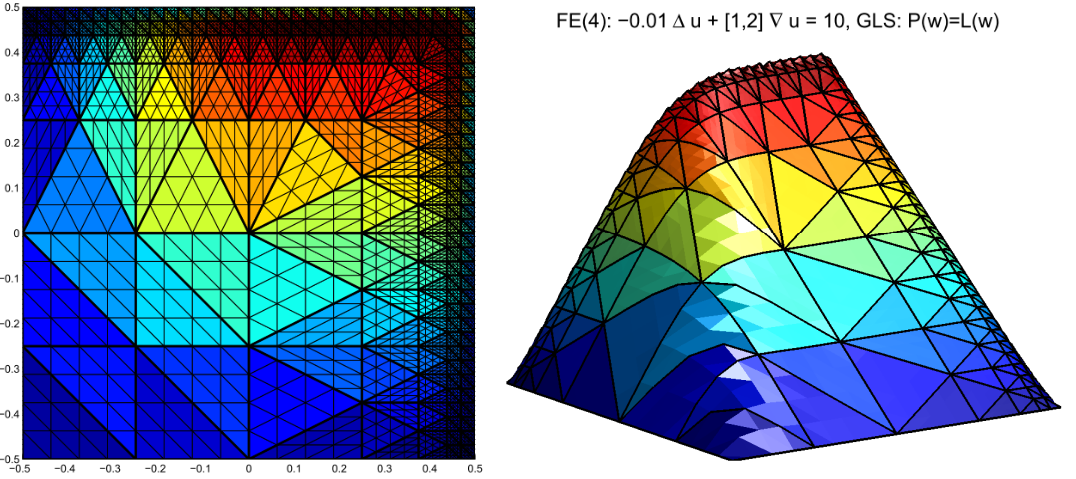
Convection-diffusion solution on a hierarchical mesh with polynomial shape functions of fourth degree.
Figure 2: Convection-diffusion solution on a hierarchical mesh with polynomial shape functions of fourth degree.
We used a Galerkin/least-squares stabilization and Gaussian quadrature of order 7.
---


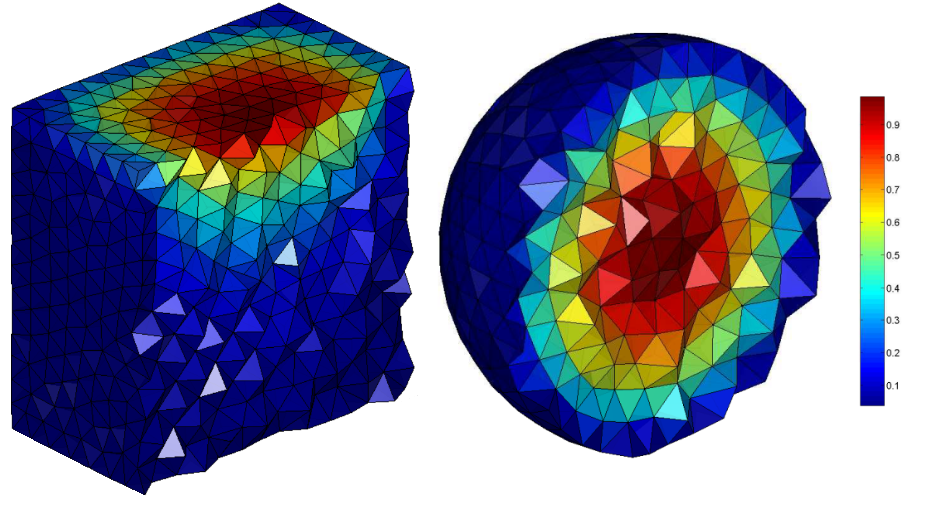
Two exemlary Poisson solutions in 3D. Left: Inhomogeneous Neumann problem. Right: Homogeneous Dirichlet problem.
Figure 3: Two exemlary Poisson solutions in 3D.
Left: Inhomogeneous Neumann problem. Right: Homogeneous Dirichlet problem.
---


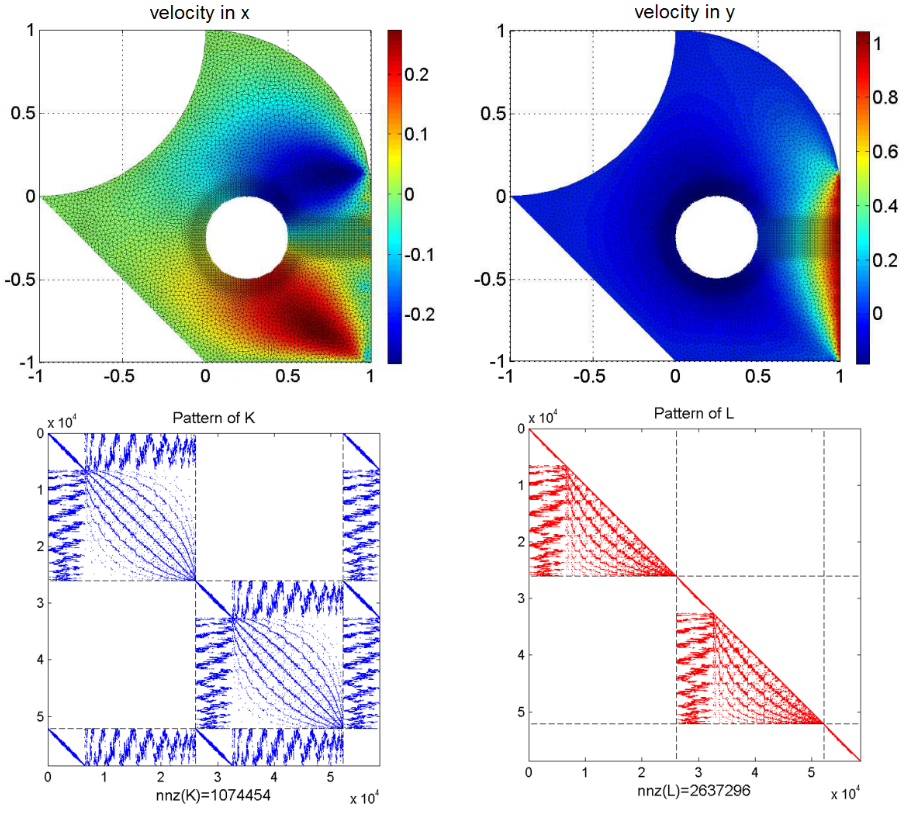
Lid-dirven cavity Stokes problem.
Figure 5: A lid-diven cavity numerical experiment for the Stokes equations. The subfigures show:
-
Top: Velocity in x and y direction of the flow field for an outer shear force at the right wall.
-
Bottom: Sparsity structures of the saddle matrix and its block preconditioner.
The blocks of the preconditioners are obtained each with an incomplete Cholesky factorization.


back to main page: Back