LSIDR(s): A least-squares variant of IDR(s)

LSIDR(s) is an interative method for the numerical computation of linear least-squares solutions. The method is an IDR(s)biortho variant applied on the Kaczmarz-preconditioned normal equations.

Motivation

For the solution of least-squares problems one usually applies an iterative solver for linear systems to the normal equations. For instance, LSQR is CG and LSMR is MINRES, each applied to the normal equations.
Both of these methods require the symmetry of A^T * A. When these methods are combined with preconditioning, e.g. a block Gauss-Seidel method for the normal equations, then this symmetry is lost. There are two approaches to overcome this issue:
  1. Replace the block Gauss-Seidel method by a symmetric block Gauss-Seidel method, which is done for instance in an SSOR-preconditioned LSQR method.
  2. Replace the iterative solver by another one which is capable of dealing with non-symmetric matrices. We did this by combining a block Gauss-Seidel preconditioner (i.e. Kaczmarz method) with IDR(s)biortho. The resulting least-squares solver we call LSIDR(s).
The advantage of LSIDR(s) compared to LSQR is, that one application of the block Gauss-Seidel preconditioner and one matrix-vector product with A cost exactly as much as as the product with A^T * A. Consequently, LSIDR(s) and LSQR have the same computational cost per iteration but LSIDR(s) is preconditioned. Thus, one would expect that LSIDR(s) converges faster. 

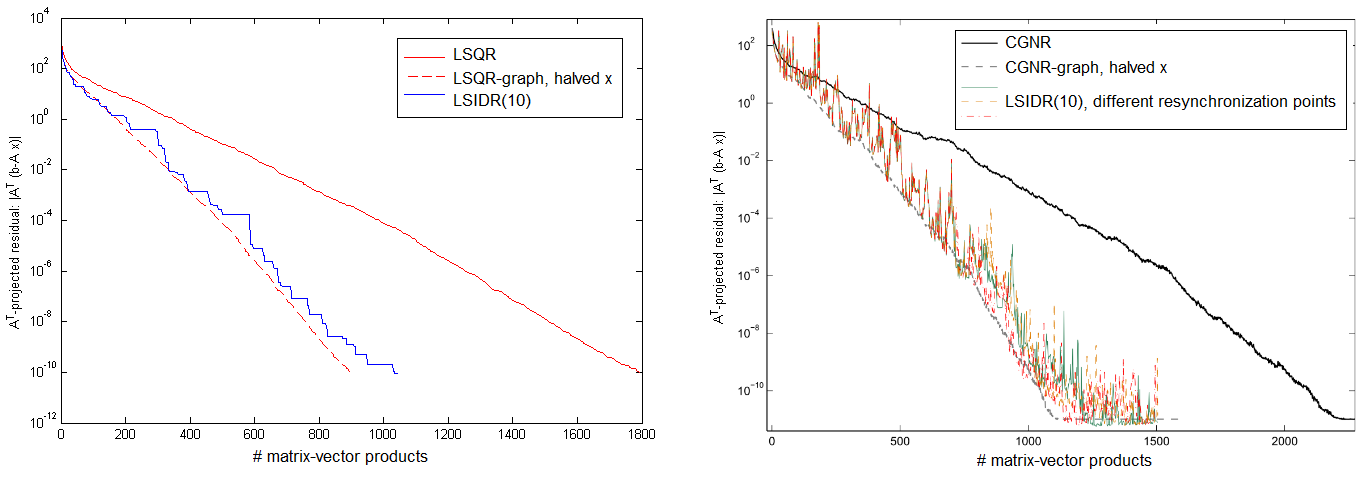
LSIDR compared to LSQR on small dimensioned dense systems with elements from a normal distribution.
Figure 1: LSIDR(10) compared to LSQR on small dimensioned dense systems with elements from a normal distribution.

The following slides give a brief description of LSIDR and an additional preconditioning concept: Slides.
Click the following link to download a (very slow) Matlab implementation of LSIDRs.
back to main page: Back