Short Recycling: Full recycling of large Krylov subspaces with limited memory and short recursions

Krylov subspace recycling is a well-known acceleration technique for the numerical solution of sequences of linear systems. With the term short recycling we want to indicate that we consider short-recurrence methods that are capable of recycling information from large-dimensioned Krylov subspaces with only limited memory and small or even without any computational overhead.

Early work

The referred report introduces the following four concepts:
  1. The recycling of Sonneveld spaces: It is possible to cheaply restrict an arbitrary right-hand side into a small-dimensioned Sonneveld space of a former solution process of a linear system. This is beneficial for an iterative method because it is a well-known experience that a smaller dimension of the Sonneveld space leads to a faster convergence (superlinear convergence). An early IDR-type method which is based on this concept is called SRIDR(s).
  2. Short Representations: This is a concept for the memory-efficient storage of basis matrices of Krylov subspaces. The concept can be used to recycle information from large Arnoldi-type decompositions, leading to the methods SRCG and SR-BiCG. One successor of these methods is SR-PCR.
  3. A stabilization approach for short representations by iteratively orthogonalizing a right-hand-side w.r.t. small blocks of a basis matrix of a test space (which is used in SR-PCR).
  4. A short recursion for the conservation of orthogonality properties of a residual which is found by the use of a short recycling method. Usually the recycling of new decent directions on a large recycled space would require long recurrences. However, by using an IDR-type post iteration method one can replace these long recursions by short ones.
The concept of Short Recycling was first presented on 24th of November 2015 at TU Delft with the following slides: Presentation .
Convergence example
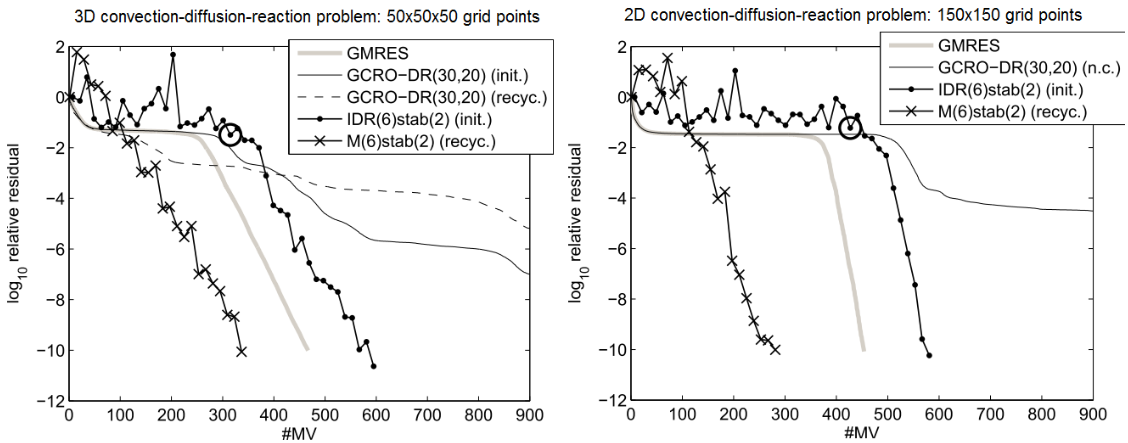
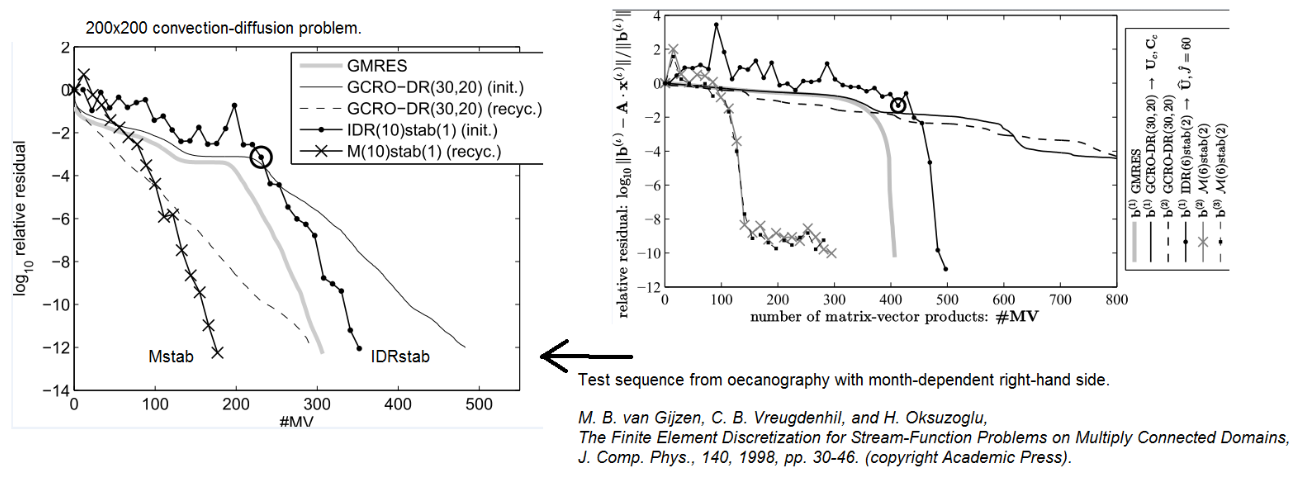
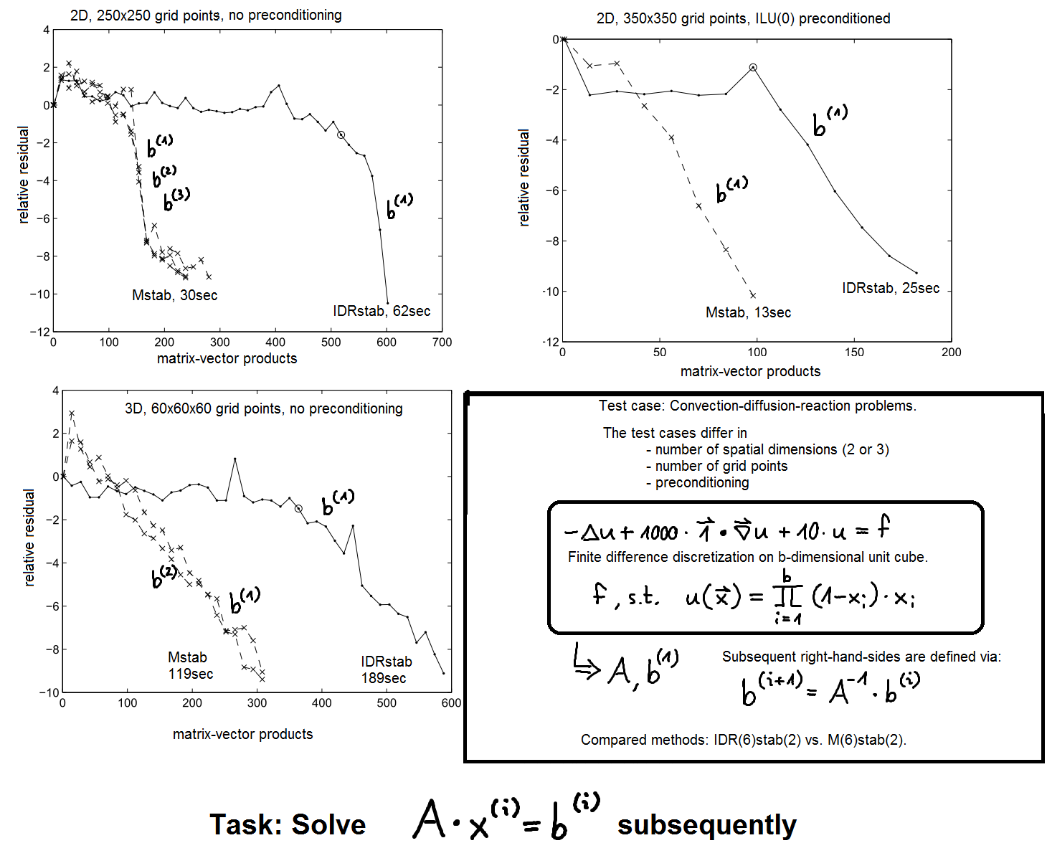
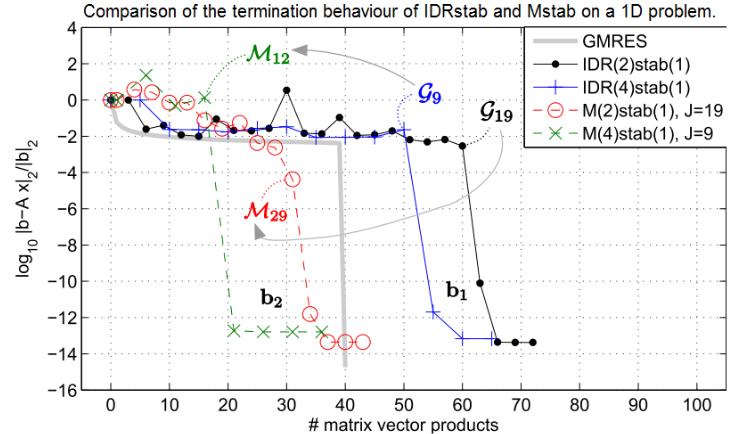
Figure 1: Exemplary convergence curves for SRIDR(10) and SRBiCG on
a 100x100 finte difference discretisation of a Poisson problem.
Fig. 1 shows the convergence behaviour SRIDR(10) and SRBiCG for a Poisson problem. One can observe that the recycling methods yield a faster convergence than their predecessors IDR(10) and BiCG. The overhead due to the recycling is 6 extra DOT products for SRBiCG compared to BiCG per matrix-vector product (#MV) during the first 40 iterations and an additional storage for 40 column vectors of length 10000. For SRIDR(10) there is no overhead at all, neither in computations nor in storage.

There are Matlab implementations for SRIDR(s) and SRBiCG : SolverPack .

Mstab: A generalization of IDRstab

Mstab applies the iterative scheme of IDRstab to a generalization of Sonneveld spaces, called M-spaces. A small-dimensioned M-space from a former solution process can be recycled easier during the iterative solution process of a subsequent linear system than a Sonneveld space. The recycling principle of Mstab can yields the advantage that Mstab converges and terminates much earlier than IDRstab.

The following figures give a first impression of the way how Mstab converges compared to IDRstab.
Numerical experiments for Mstab.
Figure 2: Redundant solution of central FD discretised PDEs. We observe that Mstab converges earlier than IDRstab.
---

Figure 3: Further test cases.

Figure 4: Comparative study of IDRstab vs. Mstab on a parametric test case.
---
Experimental verification of the termination behaviour of Mstab and IDRstab.
Figure 5: Comparison of the termination behaviour of IDRstab and Mstab.
The spaces G and M are the last spaces before the respective methods terminate.

Mstab on changing system matrices

In the following we investigate how Mstab performes if the system matrix is modified by a rank-1 or by a rank-k update. In the case of a rank-k update we assume that the k column vectors all stem from one common Krylov subspace.

Figure 6 demonstrates once again for a small dimensioned test problem and uncorrelated (namely orthogonal) right-hand sides that Mstab terminates earlier than IDRstab. On the x-axis there are markers after which Mstab would terminate if there was no round-off. Proofs for these theoretical bounds exist! Besides, one could achieve that the earlier termination is even more early by just increasing s. For the example it was chosen s=5.

One can think of some applications where such a kind of recycling under changing A is potentially useful:
  1. In SQP active set methods the replacement of one constraint by another results in a rank-1 update.
  2. In several quasi-Newton methods such as Broyden and BFGS. With BFGS one is luckily in the situation that the two column vectors of the rank-2 update stem from a common Krylov subspace.
Early termination of Mstab for changing system matrices.
Figure 6: The termination behaviour of M(5)stab(2) on a small-dimensioned test problem.
back to main page: Back